Loading... ## 前言 今天刚好看到3Blue1Brown的卷积视频[视频](https://www.bilibili.com/video/BV1Vd4y1e7pj) 然后看到做卷积的快速算法涉及到了FFT,于是就研究了半天FFT到底是什么 ## 引入 首先说明一下卷积是在做什么,3B1B这个视频主要是讲解了离散卷积 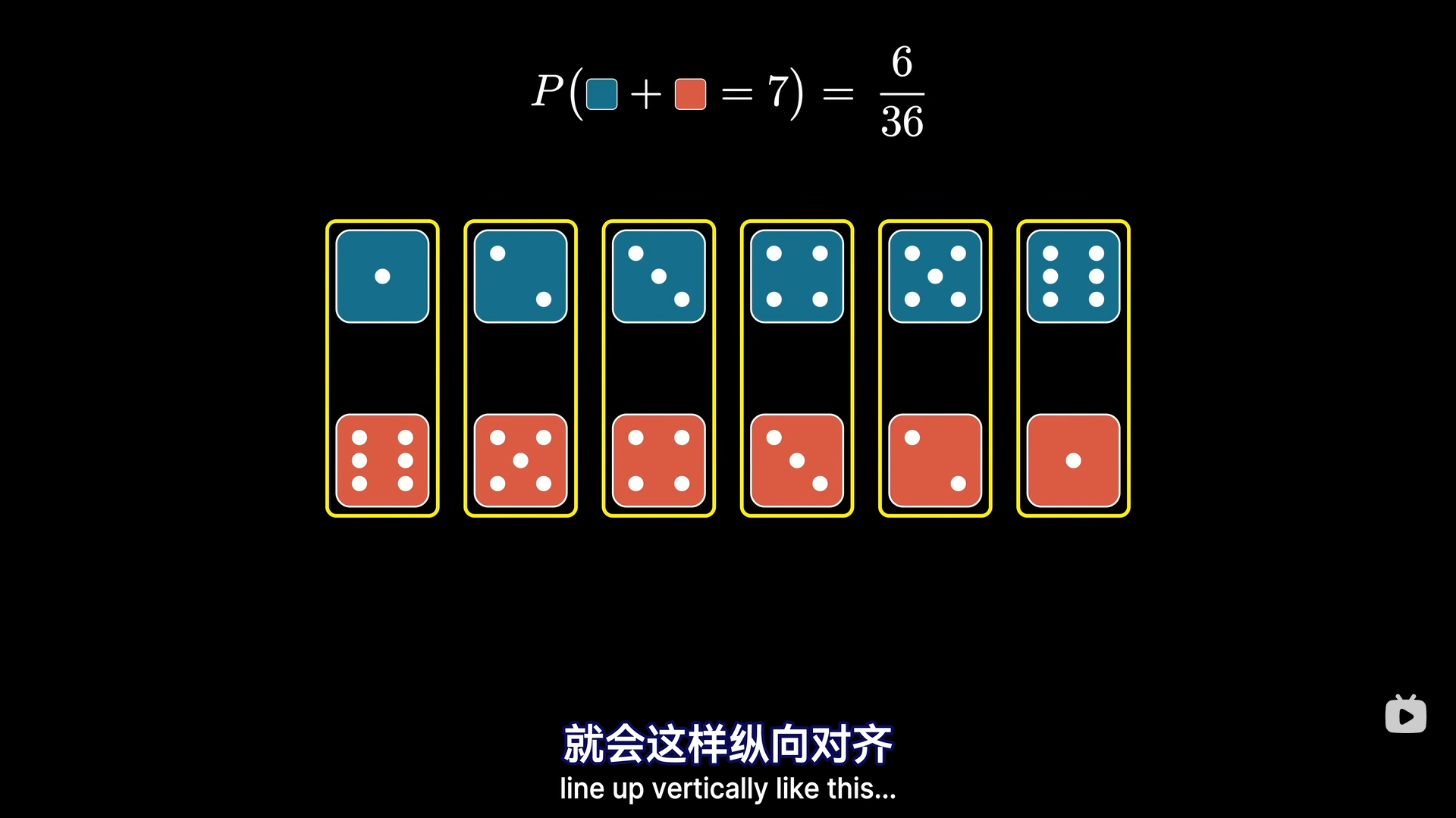 以这个色子概率问题为例子,两个色子的点数之和的求解就可以表示成卷积的形式  将一行色子倒序,然后与另一行色子进行一个类似滑动窗口匹配的形式,便可以计算卷积的结果,事实上其实就是如同上图的这样一个公式。 这便是数学定义下的卷积 那么,卷积在**实际运用**中主要用来干什么呢? 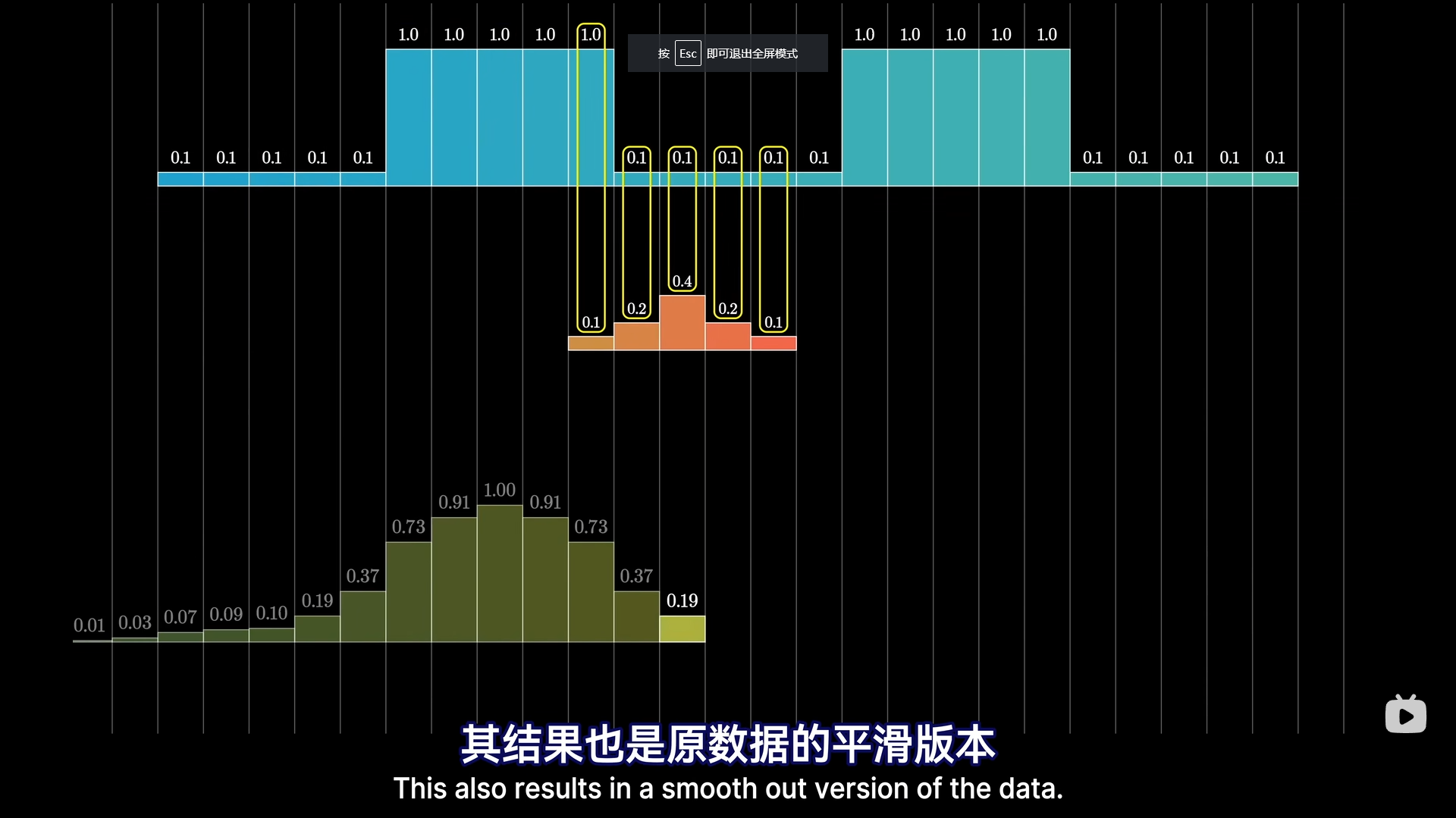 很明显可以看出,通过调整卷积核,可以使用不同的权重来获得我们想要的效果,最主要的运用便是进行平滑处理,亦或是图片的模糊处理、边缘检测、锐化处理等等   高斯分布卷积核  边界检测   图像锐化处理 这里顺带还提了卷积神经网络的目标便是通过训练来得到一个合适参数的卷积核用于检测目标 那么,我们知道了卷积在应用中是拥有着多么重要的地位,那么这里就可以抛出一个问题,**如何快速的计算卷积**,利用传统方法来计算的话,其时间复杂度高达 $O(n^2)$,于是就会思考,如何能够将卷积计算的时间复杂度降下来。  ## FFT 这就是这个文章的主题,**快速傅里叶变换**,使得时间复杂度降至 $O(nlog \ n)$ 的算法 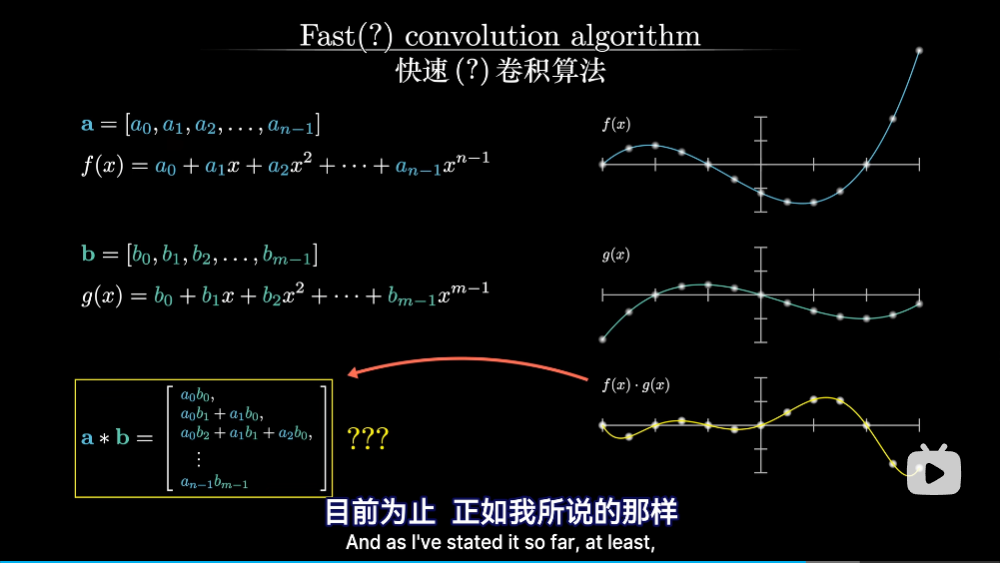 这里涉及到了定理:**任何 n + 1 个点可以确定唯一一个 n 阶函数** 那么,如上图,经过计算出足够多的点的值便可以反向恢复系数的值,也便能求出卷积的值 而如何快速计算各个点在函数的输出值,并借此反推出系数值,便是 FFT 大展拳脚的地方了。  注意到这里计算的各个点可以任意选择,那么我们就可以着手于这里来减少计算量,如何减少呢?通过奇函数和偶函数的概念,我们可以知道偶函数有如下性质: $$ f(x)=f(-x) $$ 而奇函数则是: $$ f(x)=-f(-x) $$  对于任意一个函数,都可以将其拆分成奇函数和偶函数的部分,将奇函数和偶函数分别进行计算重复的操作,对其进行二次项提取,然后接着拆分出奇函数和偶函数部分,直到剩下一项为止,反复进行这些操作,形似递归。然后通过带入相反数对,那么就可以节省许多的计算步骤  但是明显求值点都是平方数,因此都是正数,从而没办法满足相反数对的要求,那么这里就需要引入复数的概念来满足这个要求了。 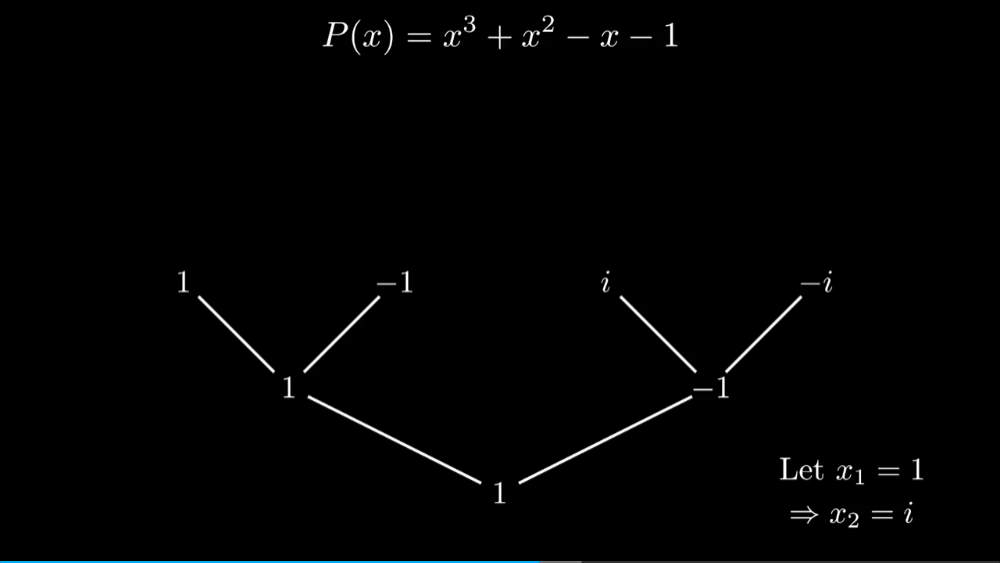 通过逆向思维,可以得到我们所需要的这几个点分别是哪些点 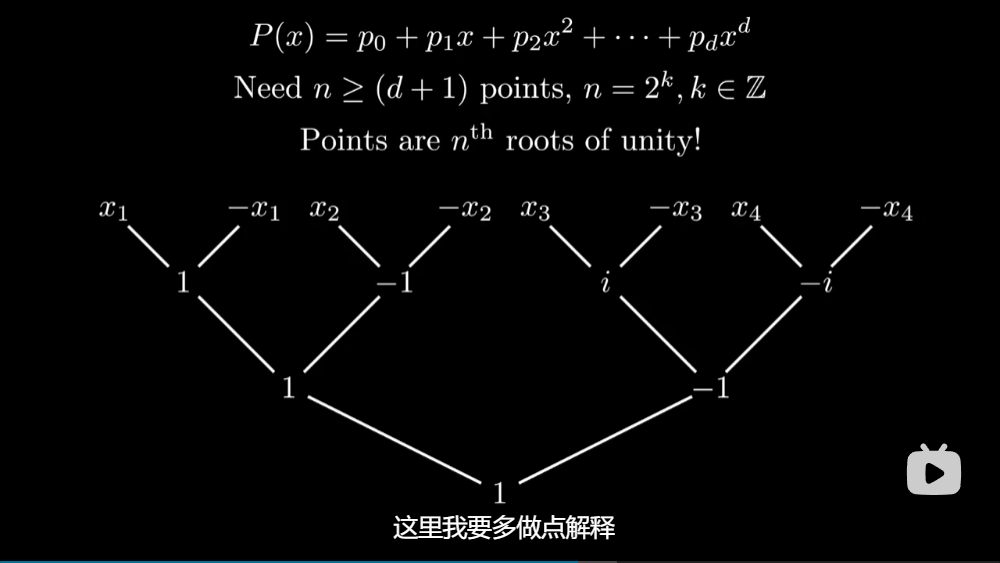 于是就可以推出这样一个规律,我们需要取的点个数,即为 $n\geq d,n=2^k$ 个,这里的 d 为函数最高次数,并且这 n 个数是 $1^n$ 的根 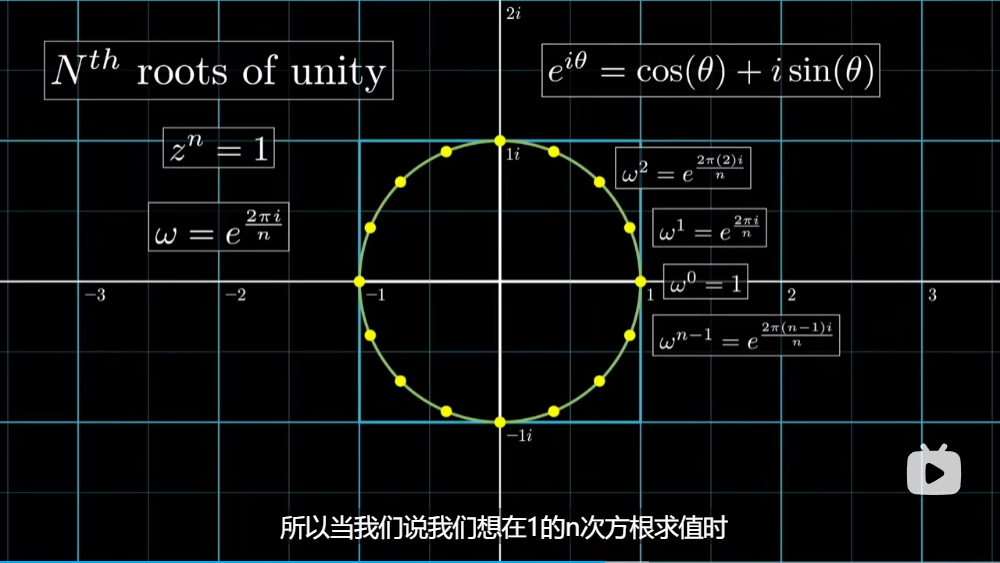 这里涉及到了欧拉公式:$e^{i\theta}=cos(\theta )+isin(\theta )$ $ 1^n$ 的根即在复平面上的单位圆上的点 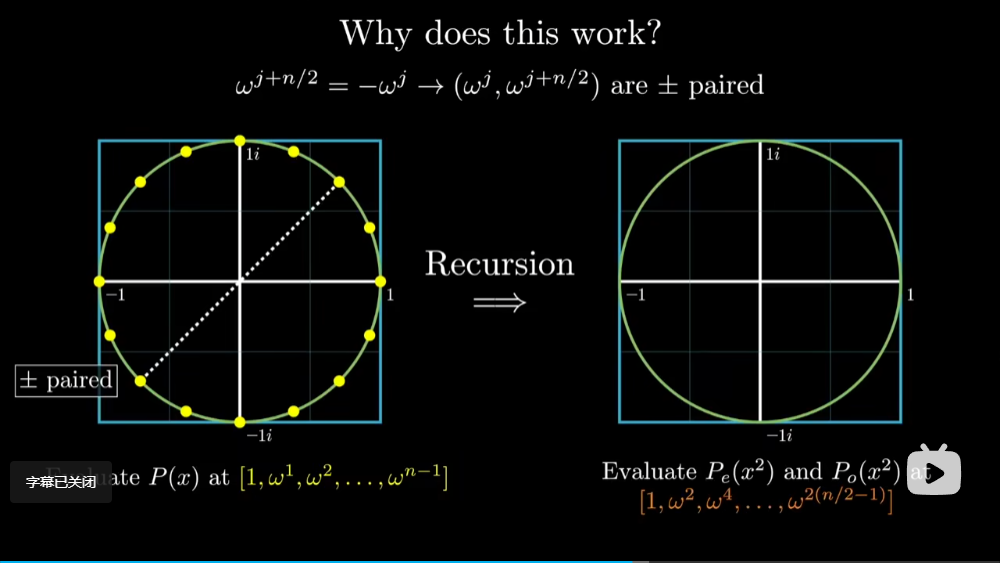 然后为了对称,可以发现$w^{j+n/2}=-w^j$,那么它们就是成相反数对的数。 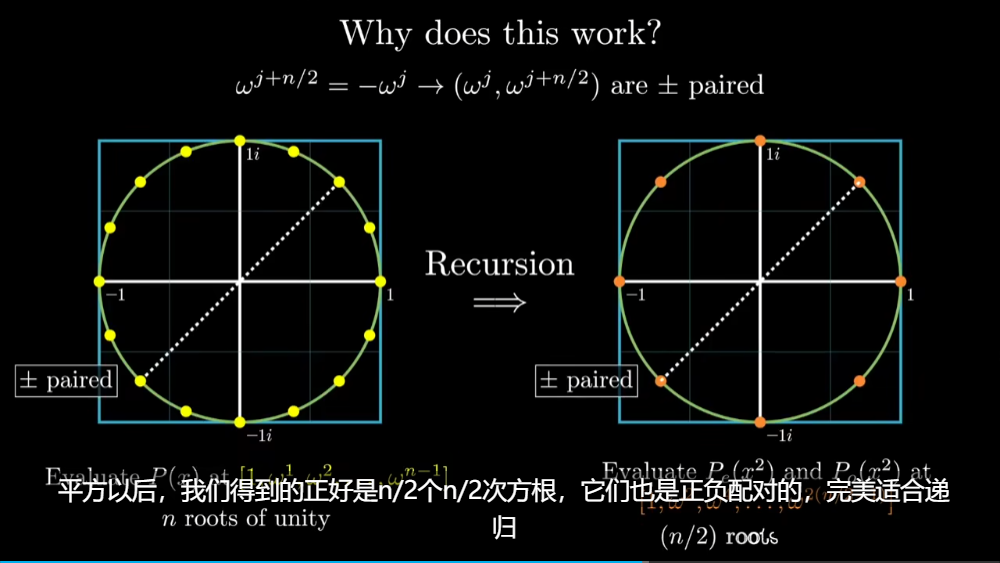 并且递归平方后,照样满足相反数对的性质,完美契合了我们所需要的条件 如下是FFT算法的整体框架,需要注意的是,如果 n 不是 2 的倍数,则需要凑到 2 的倍数  伪代码实现如下:  这样,我们就可以以极快的速度将系数转换成为输出值了,现在还差将输出值重新转换为系数,也即逆快速傅里叶变换,也就是从点到函数系数计算的过程,这里其实就是进行插值计算  而这需要我们从方程表示开始着手,也就是上述矩阵表示,而将这些 x 改为 $\omega$ 就会得到如下矩阵:  那么,所谓的从值推出系数即求逆矩阵   可以发现逆矩阵实际上就是把 $\omega$ 换成了 $\frac{1}{n}\omega^{-1}$ 于是便可以得到逆快速傅里叶变换的伪代码  **这里要注意,IFFT的 $\omega$ 需要换成 $(\frac{1}{2})*e^{\frac{-2\pi i}{n}}$ 或者 {删去 $\omega$ 的 $\frac 1 n$ 系数,然后对最后的 y 除以 n}** 到此,我们已经可以在时间复杂度 $O(N\ log(N))$ 的条件下计算卷积了。  ## 参考资料 [【官方双语】那么……什么是卷积?](https://www.bilibili.com/video/BV1Vd4y1e7pj) [快速傅里叶变换(FFT)——有史以来最巧妙的算法?](https://www.bilibili.com/video/BV1za411F76U) Last modification:December 29, 2022 © Allow specification reprint Support Appreciate the author AliPayWeChat Like 如果觉得我的文章对你有用,请随意赞赏
One comment
我暂时看不懂